The Likelihood and The Log Loss

Classifying is assgining a label y to an observation x:

    x -> y

Such a function is named a classifier:

    f_w: x -> y

The process of defining the optimal parameters w is training.

The objective of training is to maximise the likelihood:

    likelihood(w) = P_w(y|x)

And it is equivalent to minimize the negative log-likelihood:

    L(w) = -ln(P_w(y|x))

The reason for taking the negative of logarithm of the likelihood are:

• logarithm is monotonous
• it is more convenient to work with log, since the log-likelihood of statistically independant observation will simply be the sum of the log-likehood of each observation
• we usually perfer to write the objective function as a cost function to minimize

Binomial Probabilities, Log Loss / Logistic Loss / Cross-Entropy Loss

Binomial means 2 classes, 0 or 1, whose probability is p and (1 - p).

We try to get 0 and 1 as values when using a network, which is the reason to add a sigmoid function or logistic function that saturates as the last layer.

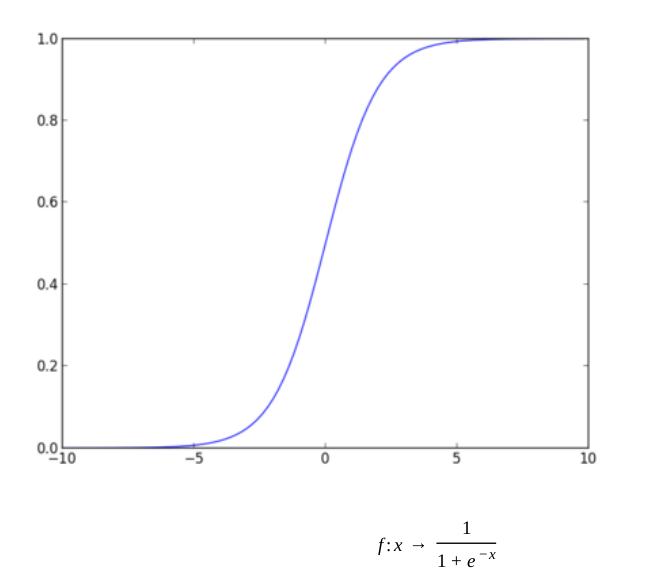
Then it is easy to see that the negative log likelihood can be written as:

    L = -y*logp - (1-y)*log(1-p)

which is also the cross-entropy

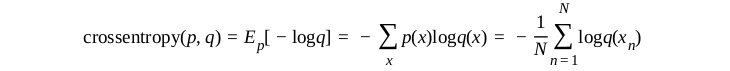
note
The combined sigmoid and cross-entropy has a very simple and stable derivative p - y.

Multinomial Probabilities / Multi-Class Classification, Multinomial Logistic Loss / Cross-Entropy Loss

The target values are still binary but represented as a vector y that will be defined by the following if the example x is of class c:

          0, if i != c
    y = {
          1, otherwise

If {p_i} is the probability of each class, then it is a multinomial ditribution and

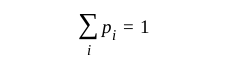
The equivalent to the sigmoid function in multi-dimensional space is the softmax function or logistic function or exponential function to produce such a distribution from any input vector z:

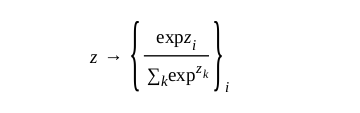
The error is also best described by cross-entropy:

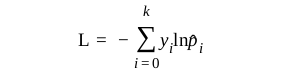
Cross-entropy is designed to deal with errors on probabilities. For example, ln(0.01) will be a more significant error than ln(0.1). In some cases, the logarithm is bounded to avoid extreme punishments.

Again, the combined softmax and cross-entropy has a very simple and stable derivative.